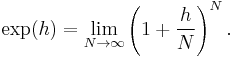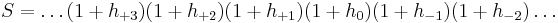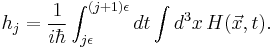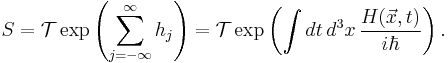Path-ordering
In theoretical physics, path-ordering is the procedure (or a meta-operator 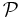 ) of ordering a product of many operators according to the value of one chosen parameter:
) of ordering a product of many operators according to the value of one chosen parameter:
Here 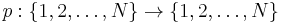 is a permutation that orders the parameters:
is a permutation that orders the parameters:
For example:
Examples
If an operator is not simply expressed as a product, but as a function of another operator, we must first perform Taylor expansion of this function. This is the case of the Wilson loop that is defined as a path-ordered exponential; this guarantees that the Wilson loop encodes the holonomy of the gauge connection. The parameter  that determines the ordering is a parameter describing the contour, and because the contour is closed, the Wilson loop must be defined as a trace in order to become gauge-invariant.
that determines the ordering is a parameter describing the contour, and because the contour is closed, the Wilson loop must be defined as a trace in order to become gauge-invariant.
Time ordering
In quantum field theory it is useful to take the time-ordered product of operators. This operation is denoted by 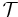 . For two operators
. For two operators 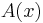 and
and 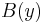 that depend on spacetime locations x and y we define:
that depend on spacetime locations x and y we define:
Here 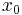 and
and 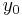 denote the time-coordinates of the points x and y.
denote the time-coordinates of the points x and y.
Explicitly we have
where  denotes the Heaviside step function and the
denotes the Heaviside step function and the 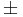 depends on if the operators are bosonic or fermionic in nature. If bosonic, then the + sign is always chosen, if fermionic then the sign will depend on the number of operator interchanges necessary to achieve the proper time ordering. Note that the statistical factors do not enter here.
depends on if the operators are bosonic or fermionic in nature. If bosonic, then the + sign is always chosen, if fermionic then the sign will depend on the number of operator interchanges necessary to achieve the proper time ordering. Note that the statistical factors do not enter here.
Since the operators depend on their location in spacetime (i.e. not just time) this time-ordering operation is only coordinate independent if operators at spacelike separated points commute. Note that the time-ordering is usually written with the time argument increasing from right to left.
The S-matrix in quantum field theory is an example of a time-ordered product. The S-matrix, transforming the state at 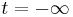 to a state at
to a state at 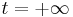 , can also be thought of as a kind of "holonomy", analogous to the Wilson loop. We obtain a time-ordered expression because of the following reason:
, can also be thought of as a kind of "holonomy", analogous to the Wilson loop. We obtain a time-ordered expression because of the following reason:
We start with this simple formula for the exponential
Now consider the discretized evolution operator
where 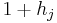 is the evolution operator over an infinitesimal time interval
is the evolution operator over an infinitesimal time interval ![[j\epsilon,(j%2B1)\epsilon]](/2012-wikipedia_en_all_nopic_01_2012/I/ec83a1a53cd2633265426997ad96448f.png) . The higher order terms can be neglected in the limit
. The higher order terms can be neglected in the limit 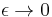 . The operator
. The operator 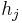 is defined by
is defined by
Note that the evolution operators over the "past" time intervals appears on the right side of the product. We see that the formula is analogous to the identity above satisfied by the exponential, and we may write
The only subtlety we had to include was the time-ordering operator 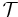 because the factors in the product defining
because the factors in the product defining  above were time-ordered, too (and operators do not commute in general) and the operator
above were time-ordered, too (and operators do not commute in general) and the operator 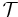 guarantees that this ordering will be preserved.
guarantees that this ordering will be preserved.
See also
- Ordered exponential describes essentially the same concept.
- Gauge theory
- S-matrix
![{\mathcal P} \left[O_1(\sigma_1)O_2(\sigma_2)\dots O_N(\sigma_N)\right]:= O_{p_1}(\sigma_{p_1}) O_{p_2}(\sigma_{p_2})\dots O_{p_N}(\sigma_{p_N}).](/2012-wikipedia_en_all_nopic_01_2012/I/d1e410918ae982af78fc236b8b1c6c3f.png)
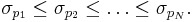
![{\mathcal P} \left[ O_1(4) O_2(2) O_3(3) O_4(1) \right]:=O_4(1) O_2(2) O_3(3) O_1(4) .](/2012-wikipedia_en_all_nopic_01_2012/I/8eddf69d873844b41bdd454a82816261.png)
![{\mathcal T} \left[A(x) B(y)\right]�:= \left\{ \begin{matrix} A(x) B(y) & \textrm{ if } & x_0 > y_0 \\ \pm B(y)A(x) & \textrm{ if } & x_0 < y_0. \end{matrix} \right.](/2012-wikipedia_en_all_nopic_01_2012/I/f2ccbcacee4dd5885a7d9b509f4c5484.png)
![{\mathcal T} \left[A(x) B(y)\right]�:= \theta (x_0 - y_0) A(x) B(y) \pm \theta (y_0 - x_0) B(y) A(x),](/2012-wikipedia_en_all_nopic_01_2012/I/daa2db7b4a6d1a3a23a84d724464e97b.png)